Finding a closest value from lookup list

user626688 · Apr 1, 2021 7:51PM

Hi, I have a requirement to find an ID from a lookup table based on the closest value. I have a main table and a lookup table. Based on the value from the main table, the query should return an ID of the closest value from the lookup table.

create table measure_tbl(ID number, measure_val number (3,2));

insert into measure_tbl values(1,0.24);

insert into measure_tbl values(2,0.5);

insert into measure_tbl values(3,0.14);

insert into measure_tbl values(4,0.68);

commit;

create table Nom_val_lkp(LKP_ID number, nom_val number(3,2));

insert into Nom_val_lkp values(1,0.1);

insert into Nom_val_lkp values(2,0.2);

insert into Nom_val_lkp values(3,0.3);

insert into Nom_val_lkp values(4,0.4);

insert into Nom_val_lkp values(5,0.5);

insert into Nom_val_lkp values(6,0.6);

insert into Nom_val_lkp values(7,0.7);

insert into Nom_val_lkp values(8,0.8);

insert into Nom_val_lkp values(9,0.9);

commit;

The result should look like:

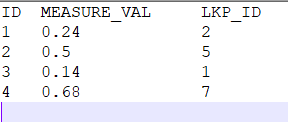How can I form a query to find a closest match of the measure value from the lookup table and pick the relevant ID in a query. Please help.

Frank Kulash · Apr 1, 2021 8:16PM

Hi,

Thanks for posting the sample data; that's very helpful!

Here's one way:

SELECT      m.id, m.measure_val
,	    MIN (l.lkp_id)
	        KEEP ( DENSE_RANK FIRST ORDER BY ABS (m.measure_val - l.nom_val))
	            AS lkp_id
FROM       measure_tbl m
CROSS JOIN nom_val_lkp l
GROUP BY   m.id, m.measure_val
ORDER BY   m.id
;

What if there's a tie for the closest value? As posted above, the query returns the lowest lkp_id that has a claim to being the closest, but that's easy to change.

mathguy · Apr 2, 2021 12:04AM

Here is a much more complicated query, which implements a different approach:

First, combine the data from the two tables (in four columns: two for the data from the first table, two for the data from the second table). Then use analytic functions, ordering the rows by the combination of values from both tables (using the nvl function). Then, for each ID from the first table, find the "bracketing rows" from the second table (closest nom_val below measure_val and closest nom_val above measure_val). In the final step, compare measure_val to the "bracketing" nominal values to see which of the two must be chosen for that ID.

In this query, the most expensive step is ordering by the combination of values from the first table. If the first table has m rows and the second has n rows, then the complexity of this operation is (m + n) * log(m + n).

On the other hand, in the solution from Mr. Kulash, the GROUP BY operation is over the cross join of the tables; this operation has complexity m * n * log(m * n). If m and n are large, this is much worse - the execution time may be much longer. Of course, you have a very easy way to tell: test on your actual data.

Here, too, in the case of ties (for "closest") some random "match" is selected. If you need to be more precise, that can be arranged - adding more information in the ORDER BY clause of the analytic functions.

with
  prep (id, measure_val, lkp_id, nom_val) as (
    select id, measure_val, cast (null as number), cast (null as number)
      from measure_tbl
    union all
    select null, null, lkp_id, nom_val
      from nom_val_lkp
  )
, bracketed (id, measure_val, last_lkp_id, last_nom_val, next_lkp_id, next_nom_val) as (
    select id, measure_val,
           last_value (lkp_id  ignore nulls) over (order by nvl(measure_val, nom_val)),
           last_value (nom_val ignore nulls) over (order by nvl(measure_val, nom_val)),
           first_value(lkp_id  ignore nulls) over (order by nvl(measure_val, nom_val)
                                 rows between 1 following and unbounded following),
           first_value(nom_val ignore nulls) over (order by nvl(measure_val, nom_val)
                                 rows between 1 following and unbounded following)
    from   prep
  )
select id, measure_val,
       case when next_lkp_id is null or 2 * measure_val < last_nom_val + next_nom_val
            then last_lkp_id else next_lkp_id end as lkp_id,
       case when next_lkp_id is null or 2 * measure_val < last_nom_val + next_nom_val
            then last_nom_val else next_nom_val end as nom_val
from   bracketed
where  id is not null
order  by id -- or by whatever; if needed
;

Paulzip · Apr 2, 2021 1:38AM

I totally agree with Mathguy that it's better to combine the two sets with union all and analytics rather than cartesian join aggregate the two sets as in Frank's solution, as it's far more scalable. It may look more complicated, but it'll pay dividends in performance and CPU usage as your datasets expand.

Here's my solution, it's akin to the approach I took for a similar problem at my company. It tries to make the result set deterministic too. If I were in your position, I might be inclined to make it into a view and then forget about it. The view would hide that complexity and you'd just select from it :

with
  combined (id, measure_val, lkp_id, nom_val, eff_id, eff_val) as (
    select c.*, nvl(id, lkp_id) eff_id, nvl(measure_val, nom_val) eff_val 
    from (
      select id, measure_val, to_number(null) lkp_id, to_number(null) nom_val
      from measure_tbl
      union all
      select to_number(null), to_number(null), lkp_id, nom_val
      from nom_val_lkp
    ) c
  )
, nearests as (
    select p.*
         , last_value(lkp_id ignore nulls) over (order by eff_val, eff_id   
             rows between unbounded preceding and 1 preceding) lte_lkp_id   -- lkp_id of closest value less than or equal (lte) to measure_val, for determinism, ties then order by id           
         , last_value(nom_val ignore nulls) over (order by eff_val, eff_id  
             rows between unbounded preceding and 1 preceding) lte_nom_val  -- nom_val of closest value less than or equal (lte) to measure_val, for determinism, ties then order by id
         , first_value(lkp_id ignore nulls) over (order by eff_val, eff_id  
             rows between 1 following and unbounded following) gte_lkp_id   -- lkp_id of closest value greater than or equal to (gte) measure_val, for determinism, ties then order by id
         , first_value(nom_val ignore nulls) over (order by eff_val, eff_id 
             rows between 1 following and unbounded following) gte_nom_val  -- nom_val of closest value greater than or equal to (gte) measure_val, for determinism, ties then order by id
    from combined p
  )
, diffs as (
    select n.*, abs(measure_val - lte_nom_val) lte_diff, abs(measure_val - gte_nom_val) gte_diff  -- Absolute differences between measure_val and the nearest lte and gte values
    from nearests n
    where id is not null
  )
select d.id, d.measure_val
     , case when gte_diff is null or lte_diff <= gte_diff then lte_lkp_id  else gte_lkp_id  end lkp_id
     , case when gte_diff is null or lte_diff <= gte_diff then lte_nom_val else gte_nom_val end nom_val
from diffs d
order by id;

        ID|MEASURE_VAL|    LKP_ID|   NOM_VAL
----------|-----------|----------|----------
         1|        .24|         2|        .2
         2|         .5|         5|        .5
         3|        .14|         1|        .1
         4|        .68|         7|        .7

Frank Kulash · Apr 1, 2021 8:16PM

Hi,

Thanks for posting the sample data; that's very helpful!

Here's one way:

SELECT      m.id, m.measure_val
,	    MIN (l.lkp_id)
	        KEEP ( DENSE_RANK FIRST ORDER BY ABS (m.measure_val - l.nom_val))
	            AS lkp_id
FROM       measure_tbl m
CROSS JOIN nom_val_lkp l
GROUP BY   m.id, m.measure_val
ORDER BY   m.id
;

What if there's a tie for the closest value? As posted above, the query returns the lowest lkp_id that has a claim to being the closest, but that's easy to change.

mathguy · Apr 2, 2021 12:04AM

Here is a much more complicated query, which implements a different approach:

First, combine the data from the two tables (in four columns: two for the data from the first table, two for the data from the second table). Then use analytic functions, ordering the rows by the combination of values from both tables (using the nvl function). Then, for each ID from the first table, find the "bracketing rows" from the second table (closest nom_val below measure_val and closest nom_val above measure_val). In the final step, compare measure_val to the "bracketing" nominal values to see which of the two must be chosen for that ID.

In this query, the most expensive step is ordering by the combination of values from the first table. If the first table has m rows and the second has n rows, then the complexity of this operation is (m + n) * log(m + n).

On the other hand, in the solution from Mr. Kulash, the GROUP BY operation is over the cross join of the tables; this operation has complexity m * n * log(m * n). If m and n are large, this is much worse - the execution time may be much longer. Of course, you have a very easy way to tell: test on your actual data.

Here, too, in the case of ties (for "closest") some random "match" is selected. If you need to be more precise, that can be arranged - adding more information in the ORDER BY clause of the analytic functions.

with
  prep (id, measure_val, lkp_id, nom_val) as (
    select id, measure_val, cast (null as number), cast (null as number)
      from measure_tbl
    union all
    select null, null, lkp_id, nom_val
      from nom_val_lkp
  )
, bracketed (id, measure_val, last_lkp_id, last_nom_val, next_lkp_id, next_nom_val) as (
    select id, measure_val,
           last_value (lkp_id  ignore nulls) over (order by nvl(measure_val, nom_val)),
           last_value (nom_val ignore nulls) over (order by nvl(measure_val, nom_val)),
           first_value(lkp_id  ignore nulls) over (order by nvl(measure_val, nom_val)
                                 rows between 1 following and unbounded following),
           first_value(nom_val ignore nulls) over (order by nvl(measure_val, nom_val)
                                 rows between 1 following and unbounded following)
    from   prep
  )
select id, measure_val,
       case when next_lkp_id is null or 2 * measure_val < last_nom_val + next_nom_val
            then last_lkp_id else next_lkp_id end as lkp_id,
       case when next_lkp_id is null or 2 * measure_val < last_nom_val + next_nom_val
            then last_nom_val else next_nom_val end as nom_val
from   bracketed
where  id is not null
order  by id -- or by whatever; if needed
;

Paulzip · Apr 2, 2021 1:38AM

I totally agree with Mathguy that it's better to combine the two sets with union all and analytics rather than cartesian join aggregate the two sets as in Frank's solution, as it's far more scalable. It may look more complicated, but it'll pay dividends in performance and CPU usage as your datasets expand.

Here's my solution, it's akin to the approach I took for a similar problem at my company. It tries to make the result set deterministic too. If I were in your position, I might be inclined to make it into a view and then forget about it. The view would hide that complexity and you'd just select from it :

with
  combined (id, measure_val, lkp_id, nom_val, eff_id, eff_val) as (
    select c.*, nvl(id, lkp_id) eff_id, nvl(measure_val, nom_val) eff_val 
    from (
      select id, measure_val, to_number(null) lkp_id, to_number(null) nom_val
      from measure_tbl
      union all
      select to_number(null), to_number(null), lkp_id, nom_val
      from nom_val_lkp
    ) c
  )
, nearests as (
    select p.*
         , last_value(lkp_id ignore nulls) over (order by eff_val, eff_id   
             rows between unbounded preceding and 1 preceding) lte_lkp_id   -- lkp_id of closest value less than or equal (lte) to measure_val, for determinism, ties then order by id           
         , last_value(nom_val ignore nulls) over (order by eff_val, eff_id  
             rows between unbounded preceding and 1 preceding) lte_nom_val  -- nom_val of closest value less than or equal (lte) to measure_val, for determinism, ties then order by id
         , first_value(lkp_id ignore nulls) over (order by eff_val, eff_id  
             rows between 1 following and unbounded following) gte_lkp_id   -- lkp_id of closest value greater than or equal to (gte) measure_val, for determinism, ties then order by id
         , first_value(nom_val ignore nulls) over (order by eff_val, eff_id 
             rows between 1 following and unbounded following) gte_nom_val  -- nom_val of closest value greater than or equal to (gte) measure_val, for determinism, ties then order by id
    from combined p
  )
, diffs as (
    select n.*, abs(measure_val - lte_nom_val) lte_diff, abs(measure_val - gte_nom_val) gte_diff  -- Absolute differences between measure_val and the nearest lte and gte values
    from nearests n
    where id is not null
  )
select d.id, d.measure_val
     , case when gte_diff is null or lte_diff <= gte_diff then lte_lkp_id  else gte_lkp_id  end lkp_id
     , case when gte_diff is null or lte_diff <= gte_diff then lte_nom_val else gte_nom_val end nom_val
from diffs d
order by id;

        ID|MEASURE_VAL|    LKP_ID|   NOM_VAL
----------|-----------|----------|----------
         1|        .24|         2|        .2
         2|         .5|         5|        .5
         3|        .14|         1|        .1
         4|        .68|         7|        .7

mathguy · Apr 2, 2021 6:18AM

https://community.oracle.com/tech/developers/discussion/comment/16790749#Comment_16790749

If I am not mistaken, your solution is identical to mine, up to rearranging things a bit.

You add ordering by eff_id in the analytic functions. In this particular query, I believe this is equivalent to ordering by lkp_id (since the rows coming from the "first table" are ignored due to the IGNORE NULLS clause anyway), so it is not necessary to define and compute eff_id in the initial subquery.

In the last part, you don't need the calls to ABS. You know beforehand that lte_diff = measure_value - lte_nom_val and gte_diff = gre_nom_val - measure_value, since in both cases you know with value is greater. And then, if you plug that into lte_diff <= gte_diff, you get exactly the inequality I wrote. This is just basic algebraic manipulation - the two formulas (inequality comparisons) are the same. For what it's worth, my reasoning for the same inequality is a bit more direct: I am comparing measure_value to the average of (that is, the midpoint between) lte_nom_val and gte_nom_val; if measure_value is to the left of this average, then it's closer to lte_nom_val, otherwise it is closer to gte_nom_val. But this different way to derive it doesn't mean that the inequality is different.

Paulzip · Apr 2, 2021 9:09AM

How is it identical to yours when it is clearly not the same - as delineated by you listing differences? Unless you mean identical in terms of result? Otherwise it seems a ridiculous comment. It was written independently - something I always like to do - and it might appear to me that you are doing a usual mathguy type response by possibly inferring otherwise.

Your nvl comment is a valid point, but I think your average approach obfuscates things.

I've been using this approach for finding nearest matches since around Oracle 9i, it's certainly not a mathguy invention.

user626688 · Apr 2, 2021 12:00PM

Hi All -

Thank you very much for the solutions!. Frank came up with a simple query, I might use solutions from Mathguy, Paulzip as the data grows and to avoid cross joins. Paulzip, thanks for adding comments!.

I appreciate everyone's help!.

Jonathan Lewis · Apr 2, 2021 1:06PM

The most appropriate answer probably depends on how accurate your model is of the thing you're really trying to do. I imagine your measures table could be very large, with more columns than you show, and maybe the numbver of lookup rows is also rather more than the 10 shown (is the measure only going to show 2 d.p. will the values always be positive - allowing for 999 non-zero values). Do you want this code to run reports that might want to select a few thousand rows and get the lookup in real time, or will you be getting just a handful of rows. The version of Oracle you're using also matters.

I thought (for entertainment only) that I'd try a different solution from the ones above - but it does assume that both the lkp_id and the nom_val have both been declared unique and non-null.

create table Nom_val_lkp(LKP_ID number not null, nom_val number(3,2) not null);
alter table nom_val_lkp add constraint nt_u1 unique(lkp_id);
alter table nom_val_lkp add constraint nt_u2 unique(nom_val);

select
        /*+
                qb_name(main)
                leading(@main [email protected] [email protected] [email protected])
                use_nl(@main [email protected])
                use_nl(@main [email protected])
                no_decorrelate(@low)
                no_decorrelate(@high)
        */
        mt.id,
        mt.measure_val,
        case
                when
                        nt_high.nom_val - mt.measure_val <=
                        mt.measure_val - nt_low.nom_val
                then    nvl(nt_high.lkp_id,nt_low.lkp_id)
                else    nvl(nt_low.lkp_id,nt_high.lkp_id)
        end     lkp_id,
        nt_low.nom_val  low_val,
        nt_low.lkp_id   low_lkp,
        nt_high.nom_val high_val,
        nt_high.lkp_id  high_lkp
from
        measure_tbl     mt,
        lateral(
                select
                        /*+ qb_name(low) index_rs_desc(nt (nom_val)) */
                        nt.lkp_id, nt.nom_val, rownum
                from    nom_val_lkp nt
                where   nt.nom_val <= mt.measure_val
                and     rownum = 1
        )(+) nt_low,
        lateral(
                select
                        /*+ qb_name(high) index_rs_asc(nt (nom_val)) */
                        nt.lkp_id, nt.nom_val, rownum
                from    nom_val_lkp nt
                where   nt.nom_val >= mt.measure_val
                and     rownum = 1
        ) (+) nt_high
/

Because of the small scale I've had to include various hints (index, use_nl, leading) to ensure that Oracle took the appropriate path - and the code ought to be explicit about order in the lateral subqueries. I've also had to add the decorrelate() hints because it turned out that I hit a bug in 12.2 and 19.3 that produced the wrong results when the optimizer tried to use the decorrelation transformation.

I was hoping that scalar subquery caching might come into play with this approach - the idea is simple even if the SQL has got a little messy (for each row run 2 simple subqueries and decide a result) but that's only a good idea if the subquery result is mostly cached and the subquery doesn't run.

My outer lateral() didn't cache when I cloned the data up to 4,000 rows, and for a very large data set it could become CPU intensive with two index probes of nom_val_lkp for every row accessed in measures_tbl.

It probably wouldn't be hard to write a version of the code that used simple scalar subqueries in the select list (rather than lateral) - and that might cache subquery results.

Regards

Jonathan Lewis

P.S. A generic detail - with a very small lookup table like yours creating the table as an index-organized table tends to give a little performance benefit - alternatively including the value as a column added to the index supporting the primary key is a simple half-way house. Both strategies allow you to avoid the extra "table access by rowid" while doing the lookup.

In this case nom_val could be the PK of the lookup table, and doing that nearly halved the work done by my version of the SQL.

UPDATE: there were a pair of result_cache hints I'd included in the code to see if I could force caching; it didn't work but I forgot to remove them (which I now have).

It only took about 20 minutes to write a version that used 4 inline scalar subqueries to get the right result. Having cloned the data 1,000 times (which resulted a big scalar subquery caching benefit) this was about twice as fast as the Mathguy/PaulZip versions, which were about 4 times as fast as the Frank Kulash solution.

mathguy · Apr 2, 2021 2:43PM

https://community.oracle.com/tech/developers/discussion/comment/16790767#Comment_16790767

Don't be ridiculous.

I wasn't implying that you copied my answer. Quite the opposite - I was implying that you may not even realize the answers are the same. Obviously I was right; even now you still think, wrongly, that they are different.

What I mean by "identical" is that you can get either answer from the other by some trivial and meaningless manipulations. If my answer says 5 - 3 and yours says abs(5-3), the answers are identical. If your answer says a - b <= c - a and mine says 2 * a <= b + c, the answers are identical. If I point that out, that doesn't mean that I am listing "differences"; I am doing exactly the opposite. And if I say 5 - 3 where you say abs(5 - 3), I don't see how my version obfuscates anything.

The only real difference is that you included an explicit tie-breaker while I only pointed it out to the OP (which Mr. Kulash had also done) as an issue to give us more clarity on.

Pointing out that another solution is the same as mine doesn't mean I claim or imply that I "invented" anything. My only claim is the one I made explicitly, which is that your solution is not different from mine.

Forum Stats

Quick Links

Categories

Finding a closest value from lookup list

Best Answers

Answers

Data

Databases

Development

Development Tools

Open Source

Programs

Forum Stats

Categories

Finding a closest value from lookup list

Best Answers

Answers